My #rEDBrum talk: The Nature of School Science Knowledge

For a while I’ve felt like school science knowledge exists as an entity, as something more than the sum of its parts, something with characteristic structure and texture. When I was planning, deciding a route through a unit, looking at links across the curriculum….I felt like I was glimpsing a sort of web, or feeling its shape in the dark and building a picture in my mind. When I was writing practice questions, I felt like I could feel different textures to the knowledge: some areas are easy to make lots of practice questions for, others are much harder. When SLT asked me to do things like chart expected progress across steps from Y7 to Y8, the structure complained – like a car being driven in the wrong gear.

I felt I had to find out more about this knowledge structure. I felt it lay at the heart of so much that we do as science teachers, and that it could explain why so much of what we are told to do is wrong. And, although I had only glimpsed it, it looked beautiful.

 

So when Adam Boxer asked me to write about the structure of knowledge for his AfL in Science Symposium, I set out to uncover it. I’ve been influenced by the work of many great people: Michael Fordham, Christine Counsell, Niki Kaiser, Tomas White, Christopher Winch, Basil Bernstein, Frederick Reif and Michael Polanyi. This talk is about the things that I found.

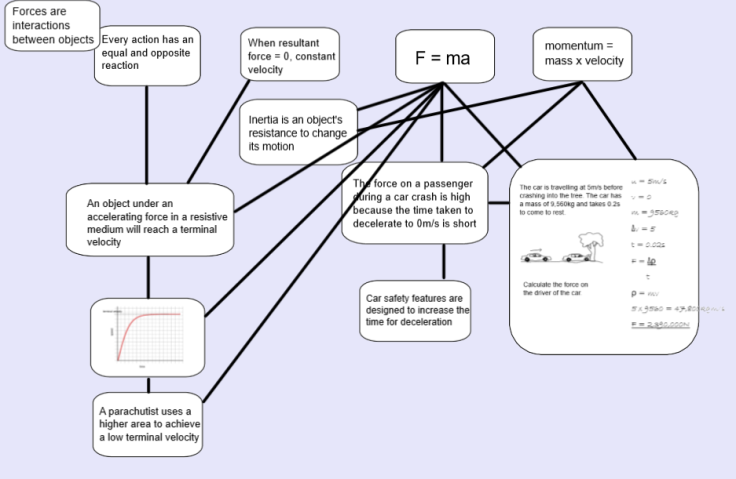
This is an example of what I think school science knowledge looks like for the “Forces” topic. Although it looks like it, this is not a concept map. It’s a knowledge map, and it behaves differently. Of course you can make concept maps for science, and they’re very interesting and useful, but it won’t show you the same things and it won’t answer the same questions. I think a concept map shows the relations between things in the world and knowledge maps show the relations between knowledge – which is located – in us –  I think. If the human race and all of our books (and data) were obliterated, but the rest of the world left intact, would our knowledge still exist? I think not – but the objects of that knowledge – gravity and atoms and so on, would. So in this scenario, knowledge maps would no longer refer to anything, at least in the present– but concept maps would.

 

I’ve studied the structure of school science knowledge, rather than scientific knowledge, for a reason. Although the two are obviously related, and have the same referents in the natural world, they are not identical. I’m concerned with school science: I’m a teacher.

 

So – the thing I’ve been studying – it’s not quite the relationships between things in the natural world – and it’s not quite scientific knowledge as used by practising scientists – it’s School Science Knowledge and it’s what we as teachers want our students to learn.

 

 

The knowledge in school science is highly inter-related. If we map the knowledge we get a web like this, with many many links between the knowledge. This is because science is an explanatory pursuit with fundamental principles and internal consistency. So a single principle, such as F = ma, is linked to a great many pieces  of school science knowledge because it is involved in their explanation. At the same time, a single phenomenon, such as terminal velocity, is linked to a great many principles since it is caused by all of them. Particles, charge, inertia and Newton’s third law for example, all join F=ma to provide a coherent explanation for terminal velocity.

This is what Bernstein refers to as a “vertical” structure and Reif as “hierarchical”. It’s important for several reasons. I think it’s fairly unique to science. It expresses the purpose of science: to explain the world and maintain internal consistency. And it makes explicit relationships which are important but often just known tacitly.

 

If we look a bit closer at this web, we can see that the “nodes” are all what we might call “propositions”. Each is a piece of knowledge. These pieces take many forms.

We have principles, or laws,  such as F=ma.    There are descriptions, such as “the force on a passenger during a crash is high because the time taken to decelerate is short”.     There are procedures, such as how to calculate the force on an object during a collision.  And there are exemplars, both for situations and procedures.

All of these pieces of knowledge, these nodes, are arranged in this structure with these links between them. I found that these links are explanatory. F = ma is linked to the force on a passenger because it contributes to its explanation. Momentum = mass x velocity is also linked to it because that is also part of the explanation. It has been suggested to me that the links be labelled with verbs to show the relationships, but I thought about it and actually I think no, the relationship is always explanatory. If there are other relationships such as “increases” or whatever, they need to be contained within a proposition, within a node. As I said before, it’s not the same as a concept map.

 

So in science knowledge maps, the relations are explanatory.

Explanation, of course, has a directionality to it: If A explains B then B is explained by A. I decided to show this by position on a vertical axis: Higher nodes explain lower ones.

 

I think there are several implications for our teaching that we can take from this vertical, explanatory structure. I think it’s a good idea to plan using these maps. They suggest things to teach that we might have forgotten about. They suggest avenues for questioning to assess understanding and deepen thinking. I think often we teach the nodes but not the links, and these maps help prevent that. I think it’s really useful to look at these when planning curriculum order, not necessarily that higher nodes should come first though, that’s often not the case, but where we decide to leave an explanation until later it becomes an informed decision. And I think it’s really helpful to share the maps with students, making the organisation of our knowledge explicit to them.

These maps are interesting when we ask “What is progress in school science?”.  As I have presented it, this map shows no indication of difficulty of the knowledge. I’ll talk more about difficulty in a bit but the thing is, even if it did show difficulty, it would not give us a model for progress. Pupils need to be taken across the map in a way that best supports its assimilation. This will sometimes but not always take us from easy knowledge to hard knowledge.

What’s more, each piece of knowledge can have many levels of difficulty. For example, changing the subject in F= ma is more challenging. I imagine these layers as ascending out of the page, in the third dimension. So we can’t really just pick two areas on the map and say “this area represents more progress has been made than this area”.

Three things I think we can say about progress in science:

1. Learning more of the map is progress
2. Relating new areas in the map to old ones is progress
3. Learning to answer harder questions on the same area of the map is progress.

So I think our assessments in science are best designed to reflect these points: Our tests should be cumulative, sampling content from areas learned earlier as well as those learned recently, we should include questions that require links to be made between areas of knowledge, and they should include questions with varying levels of difficulty. And then if a pupil achieves 80% in term one, and then 80% in term 2, then these scores indicate progress and not stagnation, because the pupil has learned more.

 

So, I wanted to look more closely at the nature of the knowledge in these webs. This is what I found.

 

Much of school science knowledge is declarative, or “knowing-that”. This applies to both the nodes and the links. We know that when resultant force = 0, the velocity is constant. We know that an object falling in a fluid will reach a terminal velocity. And we know that the one explains the other. And we seek to teach our students to know all these things.

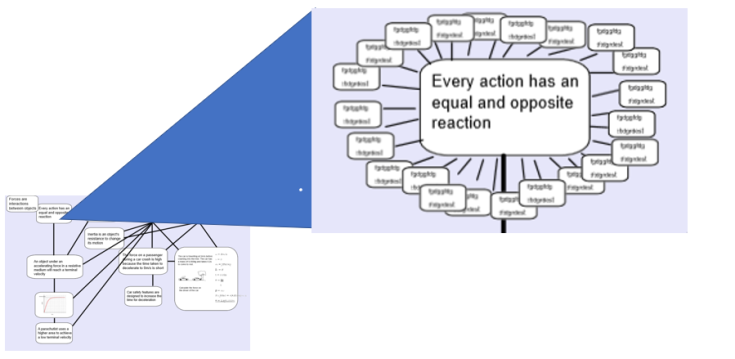
I noticed a few things about this declarative dimension. Much of the declarative knowledge has a vast, perhaps infinite, number of inferences. We could begin to show them on the map like this. So Newton’s third law here means that the ground pushes up on the chair, and the table pushes up on the book, and so on perhaps ad infinitum. This is really cool because it shows the explanatory power of science.

 

While there are a perhaps infinite number of phenomena that can be explained using the fundamental principles and entities, a more limited number of situations or phenomena are included in school science knowledge, as exemplars. These exemplars seem to be hung around the web as signposts, something we as teachers use as defining points in our teaching. I hadn’t realised before how important the role of exemplars is. They allow us to illustrate the effects of abstract principles in concrete ways. Exemplars are often an idealised situation so that the illustration of the principles concerned is optimal. Thus we are told we can “ignore air resistance”, for example. Some exemplars are demonstrations or experiments, such as the reactions of the alkali metals with water. They are often classics, shared by all who have studied the subject, and greeted with warmth by former students of school science knowledge when met again, after many years, like an old friend.

 

 

The last thing to note about the declarative dimension in science is that a lot of the propositions are counter-intuitive. In School Science Knowledge, pupils are not just learning new explanations for observable phenomena. In order to become an expert in School Science Knowledge one must successfully overcome many misconceptions, many of them I think biologically primary. For example, the misconception that a force is needed to keep an object moving is very deeply held.

 

So what does all this mean for the classroom? Well knowledge organisers are well suited to learning pieces of declarative knowledge. I set mine up in a question-and answer format to facilitate self-quizzing. With regard to the inferences bit, this is something I know my students struggle with and it’s a significant concern because of, apart from anything else, the focus in the exams on “applying to new situations”. I’ve been responding by trying to make the vast numbers of inferences explicit, both by exposing them to as many different examples as I can think of, but also just by showing them that image and telling them, this applies in more ways than we can ever list.

Planning for counter-intuitiveness, well this is the misconceptions thing isn’t it and we all know misconceptions are a big deal in science, I don’t think I’d planned well enough for them in the past though so now I’m trying a range of things like carefully sequenced examples and demonstrations to challenge misconceptions.

I found it hard sometimes, to know what exercises to give students to allow them plenty of practice in thinking about declarative knowledge? It’s much easier to create shed loads of questions for the procedural elements, which we’ll come to in a bit. But we need students to spend time thinking about this declarative knowledge because, as we know, memory is the residue of thought. So for practising declarative knowledge I’ve been looking at written exercises, getting students to write sentences of different forms using the declarative knowledge they’ve been taught. I’ve found that there is so much more to sentences than I knew, and I think it’s a promising way to practise using declarative knowledge.

 

As well as all this declarative knowledge of course then, science has a significant procedural dimension, or “knowing-how”. I think it’s fair to say that a lot of this is what we might call “formal-procedural”, as they only have one or a very small number of correct ways of being carried out. Here’s an example of a problem involving procedural knowledge: to solve it you have to know the procedure for calculating frequency. We can include balancing equations, solving free-body diagram problems, punnet squares and drawing ray diagrams in this type of knowledge.

The exact nature of procedural knowledge is interesting and not uncontroversial. Some philosophers claim that it is just a type of declarative knowledge, in that to carry out the procedure you just have to know that x is step 1, y is step 2, and so on. I believe there is something more to it, but it’s better if I return to that in a later section, so for now I’ll just say that I believe it is useful to distinguish procedural knowledge from declarative as the implications for the classroom are different. One important difference is that knowledge organisers aren’t much good here. I could get my students to self-quiz on the question “How do you find frequency if you are given the wavelength and the speed in a worded question?” But it would not do much good. Worked examples and shed loads of practice are far better. Very exciting, I think, is the process of atomisation that I’ve read about on Kris Boulton’s blog, that is to say breaking the process into steps of the smallest possible size, and making explicit all the steps that we as experts do automatically, and teaching and assessing all these steps individually before moving on to the next.

 

I feel that the nature of knowledge is defined partly by the type of questions that it answers. In school science knowledge, these questions are largely explain, describe, calculate, demonstrate, or predict. The answers to these questions are usually short, and right- or- wrong. These points are really important and, in my experience, often overlooked by trigger-happy Bloom’s enthusiasts or non-specialist observers. Feedback as a tick, if the answer is right, is appropriate for a large part of school science. We don’t need to be writing, “What went well – you got the question right”. If they got it wrong, they need more than a cross, but what they don’t need is instructions for how to improve their work: “Include more detail”; “Discuss the role of collisions”. The very idea of improving the work is wrongheaded when you look at the nature of school science knowledge: We need to improve the knowledge not the work. We need to improve the pupil’s knowledge and give opportunities to practise using that knowledge. So if a pupil gets a question wrong, we need to be able to find out precisely why they got it wrong, often through finer grain questioning, and we need to be able to correct the knowledge, and then provide plenty of practice. So what we desperately need, rather than feedback from teacher to pupil on improvements, is feedback from pupil to teacher on where a misunderstanding lies, in the form of answers to carefully designed, atomised, diagnostic questions. We need quality teacher explanations, and shed loads of practice.

I’ll just continue this rant for a bit longer if I may. Rubrics are no good for short right-or-wrong answers: what we need are model answers and worked examples. So success criteria in science  lessons are broadly irrelevant and a waste of time.

Analysis of the nature of school science knowledge shows us that we need alternative models of difficulty – things like element interactivity, recognising underlying features, abstraction and counter-intuitiveness. I’m not going to be told that my hard questions aren’t hard any more – by people who can’t actually answer them.

 

 

 

 

 

Next we come to what was, for me, the most surprising aspect of the nature of school science knowledge. The tacit dimension. The philosopher Michael Polanyi has written some fascinating work on tacit knowledge in science, and I came across it again in the work of Christopher Winch where he talks about “knowledge by acquaintance”.  Winch says of these areas of knowledge: “Description, or the use of a facsimile of some kind may approach, but will never instantiate the object under study. There is, in knowledge by acquaintance, something ineffable which resists description. This is not to say that it is a private experience, rather that it nearly always embodies a non-discursive element, which may well be part of shared experiences, but which cannot be adequately pinned down propositionally”. What Winch is saying is that the knowledge gained by seeing a person, hearing a symphony, smelling a flower or tasting a fruit cannot be described adequately using words. This is not to say it is subjective as others can experience the same thing, nor is it private as we may experience the same thing simultaneously and be aware of the other person’s experience: but it cannot be described.

I think tacit knowledge, or the fact that “we know more than we can say, as Polanyi puts it, plays a massive role in school science knowledge.

A student effectively inducted into SSK will have a relationship with the declarative principles and exemplars. He will connect with the world through the theory and the experience of doing so will be unspecifiable but important. If I were to read a news article about the invention of a perpetual motion machine I would scoff, for I am committed to thermodynamics laws. It is not an exaggeration to say that I love Maxwell’s field equations, because of the satisfaction they give me in making sense of the world I inhabit; that satisfaction is something like a sensation, it is much more than I can say. These experiences, of love and satisfaction, of connection with the universe, are of immense value in their own right. It is this that gives science its intrinsic value, independent of all the material advances it brings.

I think the tacit dimension to declarative knowledge is probably key to overcoming misconceptions, recognising underlying structures in new situations, and remembering. You never forget the people you have fallen in love with.

 

The procedural elements in school science knowledge also have a tacit dimension. When I solve a problem, I experience it. The different stages feel different to me as an impassioned participant: A business-like focus as I read through and take it in. A thrill of fear that it might be too hard. A pleasing “click” as familiar features slot in and I bring up the relevant procedures from my memory. Sparkles like diamonds because I know this way will work, but I don’t yet have the solution. A methodical, carrying-out of operations once I’ve decided what to do – this bit isn’t sparkly, it’s just an algorithm really, but it makes me happy, like colouring-in rather than creating a new painting. Conscientious laying out of my work like I learnt at 6^th form. Checking back through because god I hate that feeling when you lose a mark…. Looks right, sensible size…. Yep, it’s watertight, and I’ll double underline it to show it. These experiences form an important part, I believe, of the stages of problem solution.

 

The status of science has a tacit element too. Science has a privileged position. It is able, more than any other human endeavour, to lay claim to truth. Some disciplines are not primarily interested in the truth: art, music and literature, for example. Others are empirical and seek true descriptions and explanations: history and geography. But these other empirical subjects do not have the same privilege. A chemical analysis can prove a historical source to be a fake. A historical analysis cannot prove a scientific principle to be fake. Only more science can do that. This is not reductionism or scientism, it is not a claim that science is superior to history – each is the best we have for its purpose – but this powerful claim to truth is unique to science. This is, of course, due to the scientific method, which infuriatingly (but perhaps unsurprisingly given how much we know that we cannot say), is so difficult to define.

We can, however, describe elements that represent an ideal in science. Falsificationism, science’s appeal to experiment and observation, and the commitment to give up a theory should the evidence contradict it, is surely a demarcating ideal. Scientists certainly do not always abide by falsificationism, and indeed science would be brought to its knees if they did, since great theories are frequently contradicted by faulty evidence. But as an ideal, it is, I believe, unique to science. A historian does not do an experiment to test a theory.

Tomas White has blogged about Lakoff and Johnson’s work on conceptual metaphors, and their thesis that “human thought is governed by the often unconscious way in which conceptual domains relate to one another and that this is evident in metaphoric expressions in everyday language”.[1]

Let us see where this approach can take us with science. I think we often talk about science as an interrogation of nature by the scientist: “to make nature reveals her secrets”; “What do the results say?” “What does the graph tell us?”… I think that these metaphors reveal something of the nature of scientific knowledge, and that it is an element that has a significant tacit dimension.

 

When pupils learn science, they are being initiated, gradually, into an elite club. There is a strong tacit element to the experience of being in this club. Knowing you’re participating in a discipline that has a better claim to truth than all others, and a relationship with nature that is – what? probing, coaxing, interrogating… a questioning relationship, sometimes gentle, sometimes violent.

It has been hard for me and others to justify a lot of practical and investigative work in science due to things like cognitive load theory and the opportunity cost incurred. But I propose now that the initiation into school science knowledge is enhanced by participation in this sort of work, because of the tacit knowledge gained by the experience. The status of science as a truth-seeker is experienced passionately by the participant in a well-chosen experiment, manipulating nature to find out some truth. That feeling of your theory bumping up against nature when your results don’t fit your prediction is perhaps like how a blind man feels the pavement at the end of his stick, not the pressure on his hand where he holds the stick. This is one of the ways that Polanyi characterises how scientists experience the world through their theories. It is a tacit experience, impossible to describe in words, but very real and very important. There is an argument, then, for the novice to act as the scientist, not because it is the best way to learn some declarative or procedural knowledge, as it almost certainly isn’t, but because it is perhaps the only way to gain the tacit knowledge of science’s relationship with truth and the world. I believe this knowledge is valuable again both for its own sake and for society as a protection against charlatans and more fundamentalist strands of postmodernism.

 

 

So – what does all this mean for school science? Well first of all, we can’t test this knowledge, precisely because it’s tacit and cannot be said. But we should not think that it is unimportant because of this. We can try to express it, by describing our thought processes and our feelings when we explain phenomena, solve problems, and participate as members of the club of science.

 

 

We can choose stories and practicals for their value in developing the tacit knowledge of the status of science and its relationship with the world. We can live in an awareness of the tacit dimension and teach it even though it cannot be described in words.

 

 

So – there’s a lot to think about here. I guess the overarching points are:

If we acquaint ourselves with the nature of the knowledge in our subject, it makes the best courses of action for teaching and assessment apparent and it makes it easier to be explicit about hidden knowledge with our students

It hopefully makes us better equipped to fight against genericism, and be true to our subject.

These two points are pretty instrumentalist: they are useful to us as teachers. But I think as well, studying this structure is intrinsically fascinating. I like how it’s out there to be discovered even though it’s in here – made by us. It’s really satisfying, uncovering something that explains so much of what I’ve felt about school science in the past. And yes, I think, it’s beautiful.

 

 

 

[1] https://intheshadowoftheunthinkable.wordpress.com/